Мда, грустная тема в Паддоке.
Пока в нашей стране коррумпированность чиновников, система "купи-продай" в экономике будет выше совести и производства соответственно, такое положение вещей будет неизменным. IMHO.
Это касается не только безопасности авиаперевозок, а ситуации в целом.
А что творится на наших дорогах?
_____________________________________________________________________________________________
_____________________________________________________________________________________________
Трудно продолжать, но...
Хух...
_____________________________________________________________________________________________
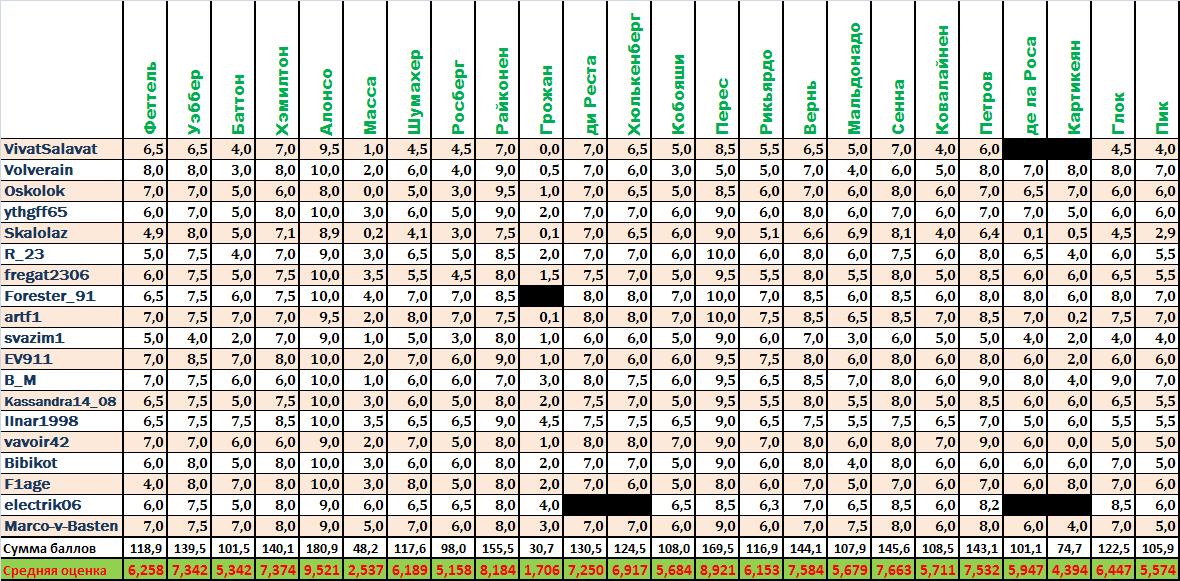
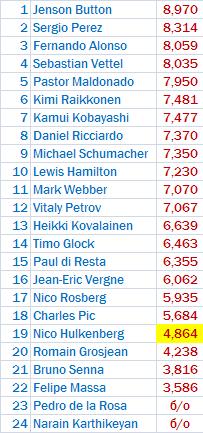
По рейтингу.
В общем помню некоторые вопросы.
Поэтому сделал небольшой стат. анализ наших оценок для определении итогового рейтинга.
Сразу таблица, потом пояснения.
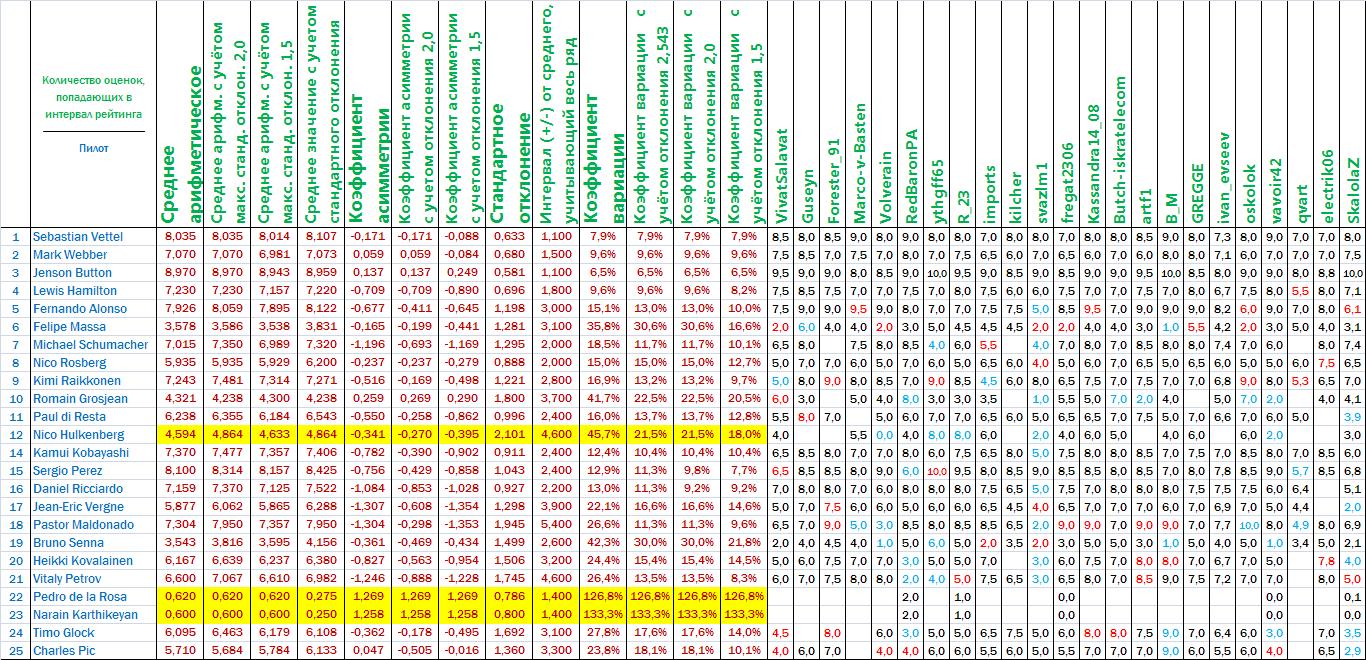
Итак, первый столбац:
"Среднее арифметическое"
Берётся общая сумма баллов и делится на общее количество респондентов.
Но средн. арифм. оценка может быть применена для однородного ряда (столбец "Коэффициент вариации").
Примечание: ряд называется однородным если коэффициент вариации ниже 35%. Если больше 35%, то неоднородный.
Для того, чтобы ряд оценок был однородным, необходимо снизить влияние так называемых "плохих" оценок (необъективность, ошибка, опечатка, условия определения и пр.)
Введение интервала/отклонения от среднего в этом случае решает задачу.
К примеру, для ряда типа 1-2-3-4-5-6-7-8-9-10 - это не подойдет. (но это не наш случай).
Здесь нужно сказать, что интервал/отклонение максимальное, при котором все ряды становятся однородными, равняется 2,543. Т.е. применение бОльшего значения недопустимо для определения среднего арифметического.
Столбец "Стандартное отклонение" нужен для определения "Коэффициента вариации".
Важным моментом также является столбец "Коэффициент асимметрии", который, в нашем случае, показывает распределение оценок.
Простыми словами, к примеру, для наглядности:
Ряд оценок 6-6-6-6-6-8 имеет положительную асимметрию.
Ряд оценок 8-8-8-8-8-6 имеет отрицательную асимметрию.
В таблице приведены расчёты "среднего арифметического", "коэффициента вариации" и "коэффициента асимметрии".
По расчетам видно, что:
При уменьшении интервала оценок "коэффициент вариации" снижается, то есть однородность ряда "улучшается".
Но при уменьшении интервала оценок значение "коэффициента асимметрии" сначала уменьшается, а потом может и увеличиваться.
Здесь скажу, что мною были исследованы интервалы с изменением в 0,1 и наиболее "подходящим" отклонением является цифра находящаяся в пределах 1,8...2,2 (среднее ~ 2,0)
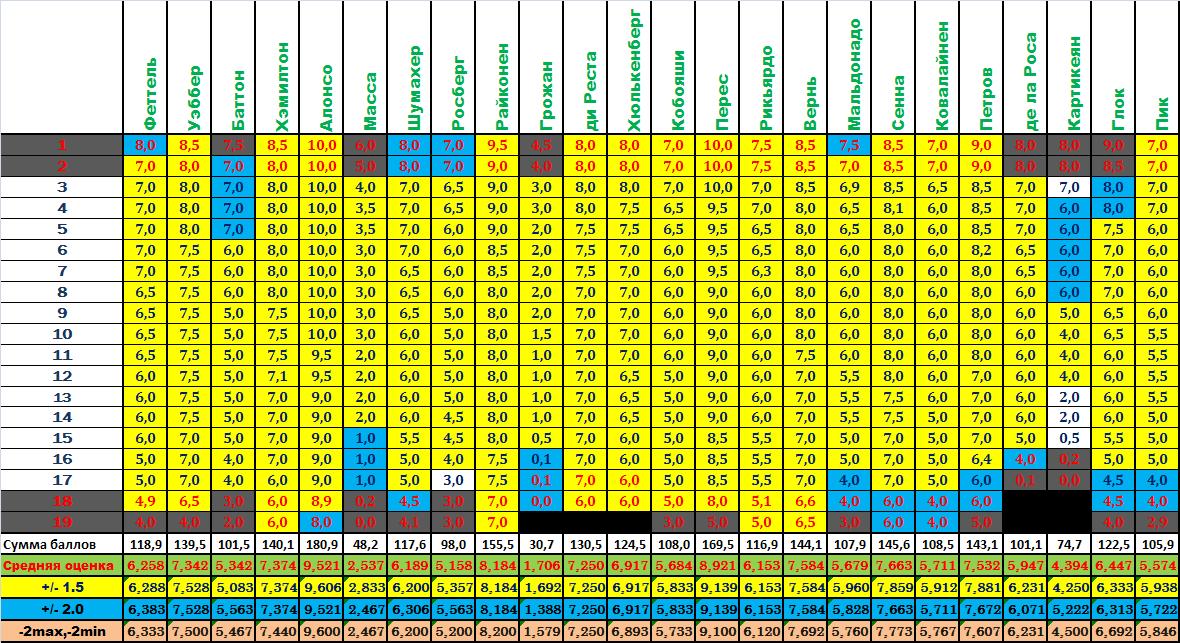
Далее: желтый фон у значений ряд оценок которых, при однородности ряда составляет менее половины от всех выборки (кол-ва юзеров). Но если Хюлкенбергу всё же можно присвоить итоговый рейтинг, то выставление итогового рейтинга пилотам ХРТ недопустимо.
Синим цветом выделены оценки не попадающие в интервал/отклонение равное 2,0.
Красным цветом выделены, дополнительно, оценки не попадающие в интервал/отклонение равное 1,5.
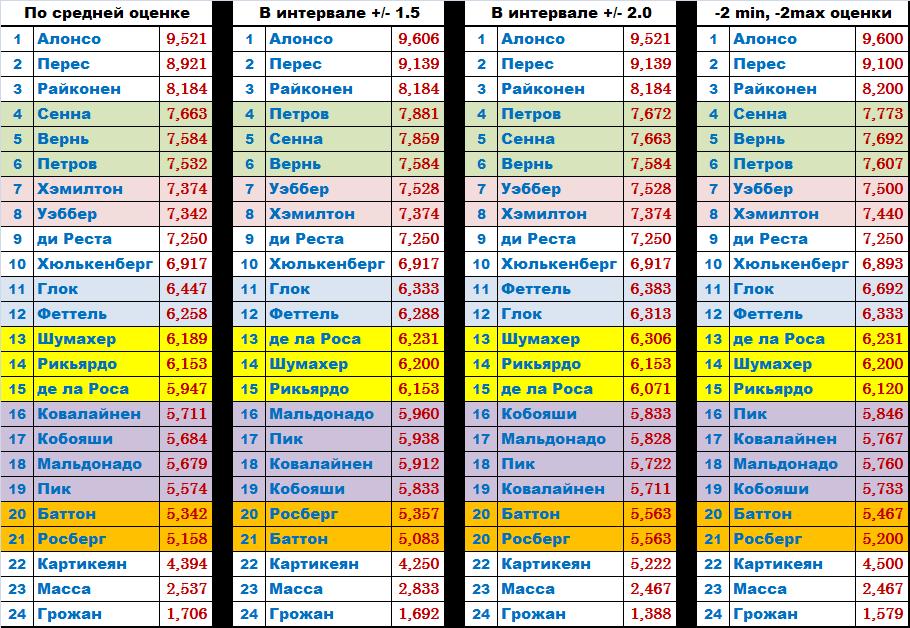
ВЫВОД: Таким образом, для определения итогового рейтинга с учетом объективности оценок, вероятности ошибок, опечаток, достаточности количества ряда оценок (выборки), однородности ряда необходимо применение интервала равного ~ 2 и применение, с учётом интервала порога оценок от общего количества респондентов ~ 40-50 %.
При применении этих показателей получается
за ГП Австралии.
PS: Этим анализом думаю смог ответить на спорные вопросы, окончательное решение за автором Григом.
Скажу сразу, что методов определения среднего значения много. Но... как упоминал GREGGE, что здесь слишком заумно не нужно, и с учётом исследованного, с этим соглашусь.


 Тема закрыта
Тема закрыта